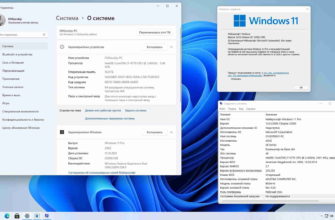
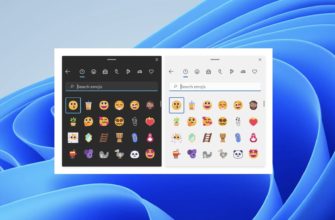
Определение. Логарифмом числа b по основанию a , где a > 0 , a ≠ 1 , b > 0 , называется показатель степени, в которую нужно возвести основание a , чтоб получить число b .
Определение. Десятичный логарифм — логарифм по основанию 10.
Другими словами, десятичный логарифм числа b является решением уравнения 10 x = b .
Обозначение. Десятичный логарифм обозначается lg x или log x .
Калькулятор десятичных логарифмов
Свойства десятичного логарифмов
lg x = log10 x — так как основание десятичного логарифма равно 10.
lg( x · y ) = lg x + lg y
lg x y = lg x — lg y
(lg x )′ = 1 x ln 10
| ∫ | lg x dx = x lg x — x ln 10 + C |
| lim | lg x = -∞ |
| x → +0 |
lg 100 = lg 10 2 = 2
lg 1000 = lg 10 3 = 3
lg 0.1 = lg 10 -1 = -1
lg 0.01 = lg 10 -2 = -2
lg 0.001 = lg 10 -3 = -3
Доказать равенство: a lg b = b lg a .
Запишем очевидное равенство:
lg b · lg a = lg a · lg ab
Возведем 10 в соответствующие степени
10 lg b · lg a = 10 lg a · lg b
(10 lg b ) lg a = (10 lg a ) lg b
Зная, что lg 2 = a , lg 3 = b , lg 5 = c , выразить lg 6; lg 30; lg 16 через a, b, c.
Используем формулы логарифма произведения и степени получим:
lg 6 = lg (2·3)= lg 2 + lg 3 = a + b ;
lg 30 = lg (5·2·3)= lg 5 + lg 2 + lg 3 = a + b + c ;
lg 16 = lg 2 4 = 4 · lg 2 = 4 a .
Вычислить log9 5 · log25 27.
Перейдем к основе 10:
log9 5 · log25 27 = lg 5 lg 9 · lg 27 lg 25
Используем свойство логарифма степени lg x n = n lg x :
lg 5 lg 9 · lg 27 lg 25 = lg 5 lg 3 2 · lg 3 3 lg 5 2 = lg 5 2 lg 3 · 3 lg 3 2 lg 5 = 3 4
Вычислить log30 8, если lg 5 = a , lg 3 = b .
Перейдем к основе 10:
log 30 8 = lg 8 lg 30 = lg 2 3 lg (3 · 10) =
Используем свойство логарифма степени, произведения, частного и то что 2= 10 5 :
= 3 lg 2 lg 3 + lg 10 = 3 lg 2 lg 3 + 1 = 3 lg 10 5 lg 3 + 1 = 3(lg 10 — lg 5) lg 3 + 1 = 3(1 — lg 5) lg 3 + 1 =
Подставим lg 5 = a , lg 3 = b :
log30 8 = 3(1 — a ) b + 1
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если b = a c c = logab, a,b,c принадлежат к действительным числам, b > 0, a > 0, a ≠ 1
a основа логарифма
Например: 2 3 = 8 => log28 = 3
Стандартное обозначение логарифма с базой 10(десятичного логарифма) и e .
Свойства логарифма
$log_a(b cdot c) = log_ab + log_ac$ показать пример
$log_afrac
$log_ab^n = n cdot log_ab$ показать пример
$log_bc = frac
$log_
e0$
loga(b ± c) — формула не существует
Антилогаритмуване
logab = logac ⇔ b = c
logab = c ⇔ a c = b, который b > 0, a > 0 и a ≠ 1
logab > logac ⇔ если a > 1, то b > c,
если 0 2 =
График логарифма
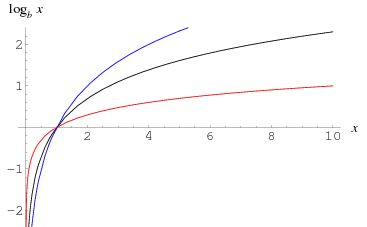
Отсюда видно, что когда x = 1 , log = 0 ; где x -> 0 => log -> -∞ ; когда x -> ∞ log -> ∞
Калькулятор десятичных логарифмов поможет найти логарифм по основанию 10
Обозначение десятичного логарифма
Для обозначения десятичного логарифма существует несколько способов:
Так же возможно написание прописными буквами.
Что такое десятичный логарифм

Десятичный логарифм очень прост для понимания. К примеру, десятичный логарифм числа 100 равен 2. А числа 100 000 — 5. Таким образом,
Здесь y — число, логарифм которого мы ищем, а x — это искомый логарифм.
То есть десятичный логарифм — это степень, в которую нужно возвести число 10 для получения исходного числа, логарифм которого мы ищем. Как мы видим, для чисел кратных 10 десятичный логарифм находится просто. Для чисел, не кратных 10 логарифм будет дробным. К примерку, десятичный логарифм числа 7 равен 0.84509804001426. И тут наш калькулятор поможет с расчетом.
Десятичный логарифм нуля не существует.
Для чисел меньше единицы десятичный логарифм отрицательный.